近期,数学系盛万成教授“黎曼双曲”团队在美国工业与应用数学学会旗下重要期刊《SIAM Journal on Mathematical Analysis》上发表了题为“Supersonic reacting jet flows from a three-dimensional conical nozzle”。该论文的第一作者为37000cm威尼斯数学系赖耕副教授,通讯作者为盛万成教授,37000cm威尼斯为论文唯一单位。

随着军事技术的不断进步,冲压式喷气发动机在航空航天和国防领域的需求在持续增长。冲压式喷气发动机主要由扩压器,燃烧室和喷管三部件组成。每个部件中都有广泛的复杂的问题需要解决。冲压式喷气发动机采用的喷管通常是拉瓦尔喷管,其射流喷出的速度达到超音速甚至高超音速,被广泛应用于现代飞行器,导弹和火箭等领域。盛万成教授“黎曼双曲”团队通过求解三维柱对称Zeldovich-von Neumann-Döring (ZND) 燃烧方程的自由边界问题,对经过三维锥形喷管的燃气超声速射流进行了分析,得到了两个重要结果。当喷管外界为真空时,该论文构造了从喷管到真空的射流问题的全局经典解(下图(左));当喷管外界不为真空,且外界气压小于管口气压时,得到了射流问题的局部经典解以及射流中拦截激波的形成机制(下图(右))。该论文主要采用特征分解的方法对上述自由边界问题的解做C1估计,进而得到全局经典解的存在性和经典解的破裂的结果。
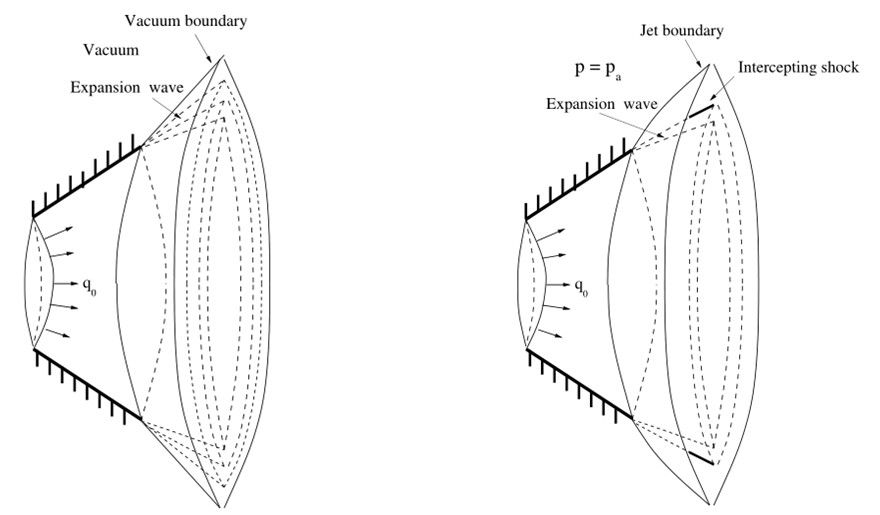
该研究工作得到了国家自然科学基金项目和上海市自然科学基金项目的资助。
37000cm威尼斯“黎曼双曲”团队2021年荣获37000cm威尼斯首届卓越导学团队(提名)荣誉称号。团队主要成员赖耕副教授是37000cm威尼斯自己培养的优秀人才(本硕博都毕业于37000cm威尼斯)。他与合作者在非线性双曲守恒律方程组二维黎曼问题、激波反射中的von Neumann悖论、绕拐角的流动问题、超声速射流等方面取得一系列重要结果,已在《Arch. Ration. Mech. Anal.》、《J. Math. Pures Appl.》、《Indiana Univ. Math. J.》、《SIAM J. Math. Anal.》、《SIAM J. Appl. Math.》、《J. Diff. Equ.》等应用数学顶级及著名期刊上发表多篇学术论文。
论文链接:https://doi.org/10.1137/22M1529099